Pisagor Nasıl Hesaplanır?
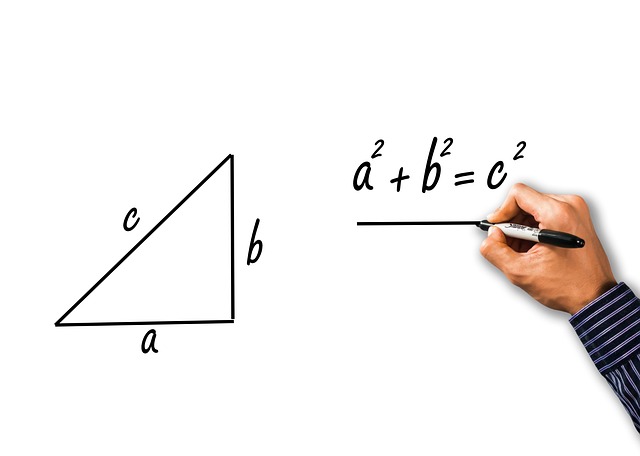
- Pisagor Nasıl Hesaplanır?
- Üçgenlerin Gizemi: Pisagor Teoremi ile Hesaplamanın Kolay Yolları
- Pisagor'un Mirası: 5 Adımda Üçgen Alanınızı Hesaplayın!
- Matematikteki Gizli Kahraman: Pisagor Teoremi Nedir ve Nasıl Kullanılır?
- Kısa Yoldan Üçgen Hesaplama: Pisagor Teoremi ile Tanışın!
- Pisagor Teoremi: Tarihsel Arka Plan ve Günlük Hayatta Uygulamaları
- Pisagor Nasıl Hesaplanır? Üçgen Hesaplamanın Altın Kuralları
- Geometriyi Eğlenceli Hale Getirin: Pisagor ile Üçgen Hesaplama Oyunları
- Sıkça Sorulan Sorular
- Pisagor Hesabını Nasıl Yapabilirim?
- Pisagor Hesaplamasında Sıklıkla Yapılan Hatalar Nelerdir?
- Pisagor Teoremi Nedir?
- Pisagor Teoremi Hangi Durumlarda Kullanılır?
- Pisagor Üçgeni Nasıl Çizilir?
Kısacası, Pisagor teoremi, dik üçgenler için geçerlidir. Bu teoreme göre, dik üçgenin kenar uzunlukları arasında bir ilişki vardır: hipotenüsün karesi, diğer iki kenarın karelerinin toplamına eşittir. Yani, a ve b dik kenarların uzunlukları, c ise hipotenüs ise formülümüz şöyle görünür: a² + b² = c². Sadece bu üç kenarın uzunlukları ile biraz matematik yaparak, dik üçgenin özelliklerini analiz edebiliriz.
Diyelim ki elimizde 3 ve 4 birim uzunluğunda iki dik kenar var. Bu durumda, bu kenarları teoremde yerine koyarsak, işlem şu şekilde gerçekleşir: 3² + 4² = c². Yani, 9 + 16 = c². Buradan c²’nin 25 olduğunu görüyoruz. Hemen ardından, c’yi bulmak için 25’in karekökünü alıyoruz ve sonuç olarak c’nin 5 olduğunu keşfediyoruz. İşte, Pisagor teoremini kullanarak kısa sürede hipotenüsü hesaplamış olduk!
Dik üçgenlerin gerçek hayattaki uygulamaları da oldukça yaygındır. İnşaat projelerinde, mobilya yerleşimlerinde hatta yolculuk planlamalarında bu teoremi kullanmak mümkün. Bir alanın köşelerinde yer alan noktaların birbirine olan uzaklıklarını bulmak, bir inşaat projesinde kesin hesaplamalar yapmaya yarar.
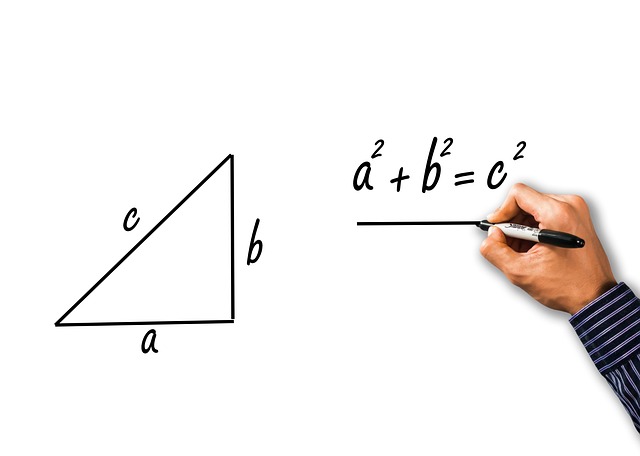
Pisagor teoremini anlamak, sadece matematik derslerinde değil, günlük yaşantınızda da size çok fayda sağlayabilir. Unutmayın; bu sadece bir formül değil, aynı zamanda bir düşünme şeklidir!
Üçgenlerin Gizemi: Pisagor Teoremi ile Hesaplamanın Kolay Yolları
Pisagor Teoremi, adını ünlü Yunan matematikçi Pisagor’dan alıyor. Bu teoreme göre, bir dik üçgenin hipotenüsü, diğer iki kenarın karelerinin toplamına eşittir. Yani, eğer a ve b üçgenin dik kenarlarıysa, c ise hipotenüs ise, a² + b² = c² formülü ile hesaplama yapıyoruz. Duydunuz mu? Bu formül, sadece bir teorem değil, aynı zamanda günlük hayatta kullanabileceğimiz bir kılavuz.
Pisagor Teoremi sayesinde üçgenlerdeki hesaplamaları yapmak oldukça pratik hale geliyor. Kendinizi bir mimar, mühendis veya günlük hayatta bir problem çözücü olarak hayal edin. Üçgenlerin alanını hesaplamak veya uzunluklarını bulmak istediğinizde, Pisagor’un formülü işinizi kolaylaştıracak. Sadece dik açı olan üçgenleri düşünün; işte burada teorem devreye giriyor! Eğer bir kenarın uzunluğunu biliyorsanız, diğeri ile hipotenüsü hızlıca hesaplayabilirsiniz. Kolay değil mi?
Düşünün ki, bir bina inşa ediyorsunuz ve yapıtaşlarının düzgün yerleştirilmesi kriter. Pisagor Teoremi devrim niteliğinde bir çözüm sunuyor. Kısacası, üçgenlerin gizemini çözmek ve bu gelişi güzel formülü hayatınızda uygulamak için tek yapmanız gereken birkaç temel hesaplama. Bu, bazen ne kadar karmaşık gibi görünse de, aslında mantık yürütmek kadar basit.
Neden siz de kendi üçgenlerinizi oluşturmuyorsunuz? Kalem ve kağıtla karşınıza çıkacak olan bu gizemi kolayca çözebilirsiniz. Matematikteki bu büyüleyici yolculuğa çıkmak için hazır mısınız?
Pisagor’un Mirası: 5 Adımda Üçgen Alanınızı Hesaplayın!
Üçgen Tipini Belirleyin: İlk adımınız, üçgenin tipini belirlemek olmalı. Eşkenar, ikizkenar ya da dar açılı mı? Hangi tür üçgenle uğraştığınızı anlamak önemlidir çünkü formüller de buna bağlı olarak değişir.
Taban ve Yüksekliği Ölçün: İkinci adım, üçgenin tabanını ve yüksekliğini doğru bir şekilde ölçmektir. Taban, üçgenin en geniş kısmı olarak düşünülürken; yükseklik, bu tabandan yukarıya doğru çizilen dik çizgidir. Bunu anlamak, alan hesabının temelini oluşturur.
Alan Formülünü Kullanın: Artık doğru ölçümlere sahip olduğunuza göre, alanı hesaplamak için formülü uygulamaya geçebiliriz. Alan, (taban x yükseklik) / 2 şeklinde ifade edilir. Bu noktada, ölçümlerinizi doğru aldığınıza emin olduğunuzdan emin olun!
Sonuçları Kontrol Edin: Hesabınızı yaptıktan sonra, sonuçları tekrar gözden geçirmek iyi bir fikirdir. Yanılma payı her zaman vardır. Özellikle sayılarda hata yapmamak için dikkatli olun.
Pratik Yapın: Son olarak, farklı üçgenlerle pratik yaparak bu süreci pekiştirebilirsiniz. Gerçekten öğrenmenin en iyi yolu deneyimdir. Hangi üçgenlerle oynadıkça, alan hesaplaması konusunda ustalaşmanız kaçınılmaz olacaktır!
Pisagor’un mirası sayesinde, matematik dünyası artık erişilebilir ve anlaşılır bir hale geldi. Üçgen alanınızı hesaplamak sadece bir formül uygulamak değil, aynı zamanda matematiğin güzelliğini keşfetmek demektir.
Matematikteki Gizli Kahraman: Pisagor Teoremi Nedir ve Nasıl Kullanılır?
Kısaca özetlemek gerekirse, Pisagor Teoremi bir dik üçgende geçerlidir. Bu teorem, dik üçgenin kenarlarının uzunlukları arasındaki ilişkiyi ortaya koyar. Bir dik üçgende, hipotenüsün karesi, diğer iki kenarın karelerinin toplamına eşittir. Yani, a² + b² = c² formülüyle ifade edilir. Burada “c” hipotenüsü, “a” ve “b” ise dik kenarları temsil eder. Şaşırtıcı değil mi? Bu basit formül, matematikte ve birçok alanda ciddi bir yer tutar.
Pisagor Teoremi, sadece kağıt üzerinde kalmaz. Mimarlık, mühendislik ve hatta bilgisayar bilimleri gibi birçok alanda uygulanır. Örneğin, bir bina tasarlarken, köşelerin doğru açılarda olup olmadığını kontrol etmek için bu teoremi kullanabilirsiniz. Bir inşaat mühendisi, bir köprü inşa ederken bu kurallar çerçevesinde çalışır; her şeyin dengeli ve güvenli olmasını sağlamak için bu matematiksel temeli göz ardı edemez.

Peki, günlük yaşamda pisagor teoremi ile karşılaşmamak mümkün mü? Kesinlikle hayır! Mesela, bir çatı inşa ederken ya da bir bisiklet sürerken bile, yolda karşılaşabileceğiniz zorlukları analiz etmek için bu teoremi kullanabilirsiniz. Kısacası, Pisagor Teoremi sadece teorik bir bilgi değil, aynı zamanda hayatın birçok alanında karşınıza çıkan pratik bir kılavuzdur!
Kısa Yoldan Üçgen Hesaplama: Pisagor Teoremi ile Tanışın!
Pisagor Teoremi, sadece matematiksel bir formül değil, aynı zamanda üçgenlerle ilgili pek çok pratik sorunu çözmede sihirli bir anahtar gibidir. İster bir inşaat projesinde ister günlük yaşamda, dik üçgenler etrafında dönen bir çok hesap yapmanız gerekebilir. Peki, Pisagor Teoremi tam olarak nedir? Temel olarak, dik üçgenlerdeki iki dik kenarının karelerinin toplamı, hipotenüsün karesine eşittir. Yani, a² + b² = c². Bunu basit bir analojiyle düşünelim: Eğer iki arkadaşınız bir çantanın içine kollarını saran bir ip gibi yan yana duruyorsa, bu iplerin toplam uzunluğu, o çantayı kaldıran merdivenin uzunluğuyla eşdeğer!
Hesaplamaları Kolaylaştırmanın Yolları ise çoğu zaman gözden kaçabiliyor. Basit bir örnek üzerinden gidelim; elimizde a = 3 ve b = 4 olan bir dik üçgen var. Bu durumda, Pisagor Teoremi sayesinde c’yi (hipotenüsü) kolayca hesaplayabiliriz. 3² + 4² işlemini yaparak 9 + 16 = 25 bulur; ardından, 25’in karekökünü alarak hipotenüsün uzunluğunu, yani c = 5 buluruz. Tüm bunları yaparken pişman olacağımız ne var ki? Hayatın her alanında karşımıza çıkan bu büyülü teoremi kullanmak, ihtiyacımız olan çözümleri sunar.
Artık üçgenlerle ilgili pratik hesaplamalar yaparken, Pisagor Teoremi’ni aklınızın bir köşesinde bulundurmak hayati bir öneme sahip. Eğlenceli bir matematik yolculuğuna çıkarken, bu teoremi kullanmayı ve onun günlük yaşamdaki kullanımını öğrenmek çok keyifli!
Pisagor Teoremi: Tarihsel Arka Plan ve Günlük Hayatta Uygulamaları
Pisagor, M.Ö. 570-495 yılları arasında yaşamış olan Yunan bir matematikçi ve filozof. Teoreminin ilk formları, antik uygarlıklardan bu yana bilinse de, Pisagor’un ismi ile özdeşleşmesi onun matematiğe olan katkıları sayesinde olmuştur. Mezopotamya ve Mısır medeniyetlerinde bile benzer ilişkilere dair kanıtlara rastlamak mümkün! Yani, bu tanımın kökleri oldukça derinlere iniyor. Pisagor’un Öğrencileri ise bu bilgileri daha da derinleştirerek, matematiksel düşüncenin temellerinden birini atmışlardır.
Şimdi gelelim bu teoremin günlük hayatımızdaki yerlerine! Bir inşaat projesi yaparken, keskin bir köşe oluşturmak için duvarları ölçmek zorundasınız. İşte burada Pisagor Teoremi devreye girer. Üçgenlerin kenar uzunlukları ile hesaplamalar yaparak, alanlarınızın simetrik olup olmadığını kontrol edebilirsiniz. Diyelim ki bir bahçe dizayn ediyorsunuz; yine bu teorem yardımıyla bitkilerinizi yerleştirirken en doğru açıyı bulabilirsiniz.
Pisagor Teoremi tarih boyunca matematikte devrim yaratmış ve her daim yaşayacak bir miras bırakmıştır. Matematiği seviyor ya da hayatınıza entegre etmek istiyorsanız, Pisagor’un dünyasına dahil olmaktan çekinmeyin!
Pisagor Nasıl Hesaplanır? Üçgen Hesaplamanın Altın Kuralları
Örneğin, bir dik üçgende kenar uzunlukları 3 ve 4 birimse, bu durumda hipotenüsü bulmak için Pisagor formülünü kullanıyoruz. Yani, 3² + 4² hesaplanır. Bu da 9 + 16 = 25 eder. Peki, 25’in karekökünü alırsak ne olur? Evet, 5! İşte, hipotenüsün uzunluğu 5 birimdir. Bu kadar basit değil mi?
Üçgen Hesaplamanın Altın Kuralları diye bir şey var ki, bunlar sizi geometrinin derinliklerine sürükler. İlk kural, her zaman dikkatlice ölçüm yapmaktır. Yanlış bir ölçüm, tüm hesaplama sürecini alt üst edebilir. İkinci kural ise, üçgenin tipini belirlemektir. Dik üçgen mi, yoksa diğer üçgen türlerinden biri mi? Çünkü Pisagor Teoremi yalnızca dik üçgenler için geometrik bir anahtardır.
Ayrıca, üçgenin kenar uzunlukları arasında her zaman bir tutarlılık olmalıdır. Yani, kenar uzunlukları arasındaki oranı düşündüğünüzde, hangi tarafın hangi tarafa karşılık geldiğini anlayabilmelisiniz. Eğer bu kuralları takip ederseniz, üçgen hesaplamalarında bir maestro gibi hareket edersiniz. Unutmayın, her üçgen hikayesini anlatır; bu hikayeyi doğru bir biçimde okumak içinse Pisagor’un sırlarına hakim olmak şart!
Geometriyi Eğlenceli Hale Getirin: Pisagor ile Üçgen Hesaplama Oyunları
Üçgenler, geometri dünyasının en temel şekillerinden biri ve onlarla oynamak, matematiği daha anlaşılır hâle getirebilir. Peki, Pisagor Teoremi nedir? Kısaca söylemek gerekirse, bu teorem, bir dik üçgenin kenarları arasındaki ilişkiyi açıklıyor. Matematik dersinde sıkça rastladığınız “a² + b² = c²” ifadesi, işte tam olarak bu. Ama size burada bir sır vereyim: Bu formülü ezberlemek zorunda değilsiniz; onu oyunlarla öğrenebilirsiniz!
Bir üçgen hesaplama oyunu düşünün. Arkadaşlarınızla bir araya gelip, farklı dik üçgenler çizebilir ve ardından kenar uzunluklarını tahmin edebilirsiniz. Her doğru tahminde, birkaç puan kazanın ve en yüksek puanı almak için rekabet edin! Bu sadece eğlenceli bir aktivite değil; aynı zamanda Pisagor Teoremi’nin pratikte nasıl işlediğini anlamanızı da sağlar.
Bir başka eğlenceli alternatif ise, online oyun platformlarında mevcut olan interaktif üçgen hesaplama oyunları. Bu oyunlar, gerçek zamanlı geri bildirimle etkileşime geçmenizi sağlar ve öğrenim sürecini hızlandırır. Örneğin, belirli bir üçgenin uzunluklarını verdiğinizde, diğer kenar uzunluklarını hızlı bir şekilde hesaplayarak sonuçları görebilirsiniz.
Peki, neden bu eğlenceli yöntemleri tercih etmelisiniz? Çünkü eğitim sadece kitaplarda değil, aynı zamanda etkileşim ve deneyimle de öğrenilir. Pisagor ile üçgen hesaplama oyunları, hem eğlenceli hem de öğretici bir deneyim sunarak sizi geometri dünyasında özgürce dolaşmaya teşvik eder.
Sıkça Sorulan Sorular
Pisagor Hesabını Nasıl Yapabilirim?
Pisagor teoremi, dik üçgenlerdeki kenar uzunlukları arasındaki ilişkiyi belirler. A, B ve C kenarlarını temsil eden dik üçgende, C hipotenüs olmak üzere, A² + B² = C² formülü kullanılarak hesaplama yapılır.
Pisagor Hesaplamasında Sıklıkla Yapılan Hatalar Nelerdir?
Pisagor teoremini kullanırken en yaygın hatalar, formülü yanlış uygulamak, kenar uzunluklarını karıştırmak ve üçgenin hipotenüsünü bulurken yanlış değerler kullanmaktan kaynaklanır. Doğru sonuçlar için, kare alma ve kök alma işlemlerini dikkatlice yapmak önemlidir.
Pisagor Teoremi Nedir?
Pisagor Teoremi, dik üçgenlerde hipotenüsün karesinin, diğer iki kenarın karelerinin toplamına eşit olduğunu ifade eder. Yani, a^2 + b^2 = c^2 şeklinde formüle edilir. Burada c, hipotenüs; a ve b ise dik kenarlardır. Bu teorem, geometri ve trigonometri alanlarında önemli bir yere sahiptir.
Pisagor Teoremi Hangi Durumlarda Kullanılır?
Pisagor teoremi, dik üçgenlerin kenar uzunlukları arasında ilişki kurmak için kullanılır. Bu teorem, bir dik üçgende hipotenüsün karesinin, diğer iki kenarın karelerinin toplamına eşit olduğunu belirtir. Genellikle inşaat, mühendislik, fizik ve geometri alanlarında dik üçgenler ile ilgili hesaplamalarda uygulanır.
Pisagor Üçgeni Nasıl Çizilir?
Pisagor üçgeni çizmek için öncelikle bir dik üçgen oluşturmalısınız. Bir dik kenar uzunluğunu belirleyin. Daha sonra, dik kenarın diğer ucundan 90 derece açıyı sağlamak için bir doğru çizin. Bu doğruyu, uygun uzunluktaki diğer dik kenarı oluşturacak şekilde işaretleyin. Son olarak, dik kenarların uçlarından birleştirerek hipotenüsü çizin. Böylece Pisagor üçgenini tamamlamış olursunuz.